The harmonic structure known as a minor 7th #5 chord (m7#5) is a relative obscurity in modern music. This is likely due to the fact that it is not a naturally occurring chord in the major scale or any of the principal minor (harmonic, melodic) scales. Another explanation is because generally when“#5” is mentioned musicians often assume an augmented chord containing a major 3rd , 1-3-#5.
The minor 7#5 chord discussed in this article is very different from the augmented formula as it has a minor 3rd instead of a major 3rd. The formula for a minor 7#5 chord is as follows: 1-b3-#5-b7; or with C as its root: C, Eb, G#, Bb. The resemblance to the standard minor 7th chord should be very clear, as only the fifth is raised one half step, or one fret in terms of the guitar.
Two types of chord voicings are presented, these are “open position”, meaning all chord tones are sounded with some note(s) more than an octave above the lowest tone; and “close position” where all tones are sounded within the space of an octave or less.
The open position chords have a guitar-like sonority due to their intervallic arrangement. The close position chords have a more pianistic quality, especially in high registers, due to the intervals being arranged in sequential order and fitting within an octave.
It is not possible to predict which chord voicing type will perform best in any given situation; one should use the ear as the ultimate judge. It is generally found that the close position chords in higher registers will tend to work better when bass and other chordal accompaniment is present, due to the span of notes not exceeding the octave.
The open positing chords have a wider spread of notes and are useful in solo situations or when no other chordal instrument is present.
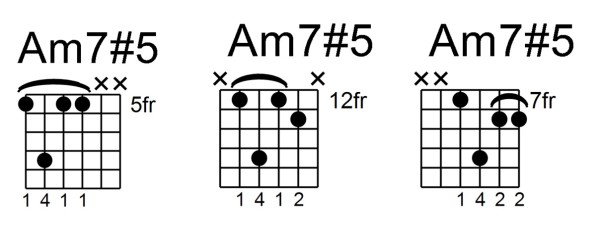
The voicings shown in Figure A are minor 7th shapes with the raised 5th, you should be familiar with these “drop 2” chord shapes.
Figure A: Open-position voicings derived from minor 7th drop 2 chord shapes.
As a review, drop 2 chords are those that have been subject to intervallic rearrangement in order to facilitate easier fingering and a more “open” sonority. The order of notes in the Figure A chord shapes is: 1-#5-b3-b7. Note that each chord is on a different string set. Memorizing these shapes makes for more efficient playing horizontally across the fingerboard versus playing vertically.
In Figure B, a more pianistic arrangement of notes is used, thus yielding a close-position chord voicing (where the notes all fit within an octave) in contrast to the shapes in Figure A. Depending on the physical location of where they are played, these chords present a considerable challenge for left-hand stretching. The end result will be worth the effort.
Figure B: Close-position voicings with a pianistic sonority and stretched fingering.
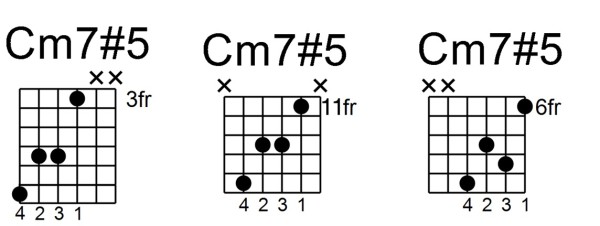
Chords shown in Figure C are voicings that use all six strings of the guitar thus producing a very rich texture. These chords do have doubled notes; the first chord has the following order of notes: 1-b3-#5-b3-#5-b7. The 3rd and 5th are both doubled and this shape is useful if a b7 melody note is desired. The second minor 7#5 chord shape has the following note order: 1-#5-b7-b3-#5-1.
The root and #5 are the only doubled tones and this chord has a strong tonic association due to its use of the root on the top and bottom strings (this intervallic width is known as a double octave or 15va).
Figure C: Six string voicings yield a rich texture for chord solos.
The first musical example, Figure 1, demonstrates the most basic use of the m7#5 chord, which is as a chromatic modification of the minor 7th chord. Experiment on this passage with straight and swing feels, differing dynamic levels, and syncopated accents. One will recognize the harmonic i-iv-v progression adapted from the minor blues style.
In Figure 2 a different approach is taken to a similar concept. Instead of changing chords after the m7#5, the #5th is raised to create a major 6th. After this chromatic ascent of the 5th, a descent occurs to a repeat. Experiment with the arpeggiated figure by playing as written but also letting notes ring out.
The m7#5 chord has another primary use. This lies in its ability to function as a first inversion major Add9 chord. The major Add9 has the following formula: 1-3-5-9. However, in the case of using the m7#5 we will generate the first inversion of the major Add9 whose formula is: 3-5-9-1.
The voicings shown in Figure A depict a different formula: 3-1-9-5. This is due to the chord being derived from a drop 2 voicing. Chords in Figure B have a different formula of: 3-5-1-9. And the chords shown in Figure C have the formula of: 3-5-1-5-1-9 and 3-1-9-5-1-3, respectively.
A simple and effective way to remember which note is the root of the major Add9 in question is to look to the 2nd note (from lowest) for chords in Figure A, and the 3rd note (from lowest) for chords in Figure B.
The next musical example, Figure 3, shows this theory put into practice by using a I-IV-V-bVI-I progression in G.
The bVI chord is borrowed from the parallel minor key of G minor, if analyzing as being borrowed from G minor we would have a III/i chord but bVI is much quicker to write and explain.
When using the m7#5 chord as a first inversion Add9, the chord may also have the major 7th tone added to create the richer and denser harmonic structure of a first inversion major 9th chord with the formula: 3-1-9-5-7. Only two of the six shapes given will feasibly function in this way due to fingering restrictions. Figure D shows the standard chord voicings with additional major 7ths (hollow circles).
Figure D: First inversion major 9th chords, note additional major 7th tones added.
The musical example in Figure 4 demonstrates descending by whole steps until an ascent by a half step at the end. This example exclusively uses the first inversion major 9th chord on different string sets.
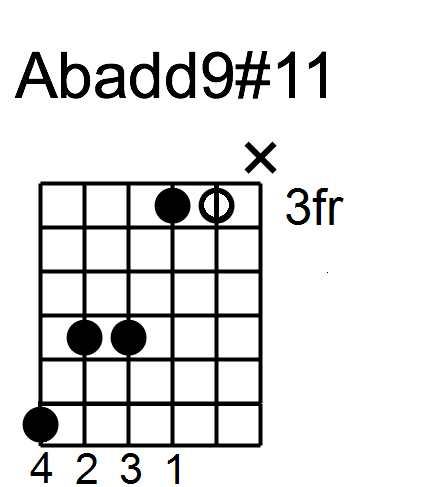
Figure E shows that when the second string is barred in the first chord shape from Figure B, we can achieve a new sonority by the addition of a #11th tone above the chord root on string 4. This yields a first inversion major Add9 #11 chord with the following formula: 3-5-1-9-#11.
Figure E: First inversion Add9 #11 chord shown with the Ab root on 4th string.
In Figure 5 we begin to interject other chords among the m7#5 chords we have been focusing on thus far. In any application of a new chord or technique it is imperative to bring the new concept out of isolation and into real-world musical scenarios. Note the heavy use of inversions played throughout the example to achieve smoother bass lines for more subtle progression of chords.
A key analysis of Figure 5 shows that the example has the key signature for Eb major while the emphasis leans toward the Abadd9#11. This shows that we are in modal territory of Ab Lydian, which has the same key signature as Eb. Otherwise the #11 would not belong to the scale if used the Ab key signature (Bb, Eb, Ab, Db).
The harmonic analysis shows quite a conservative modal approach; notice the lack of accidental notes until the last measure. We begin with the I add9#11 or Abadd9#11 which is in first inversion (C, Eb, Ab, Bb, D) the C bass changes to Ab and becomes a root position Ab6#11 chord (Ab, Eb, F, C, D).
Measure 2 moves to the V maj9, which due to the construction of the Lydian mode is not a dominant 7th variety as encountered in the Ionian (major) mode.
This chord is in its first inversion as well (G, Eb, F, Bb, D) and coming from the previous Ab bass note to this G is a smooth transition. A vi m7 chord follows with Cm7 in root position (C, G, Bb, Eb) where the bass ascends a familiar fourth, then a vii m7 as a first inversion Gm7 (Bb, D, G, Bb, D) where the bass line smoothly moves down a whole step.
From measure 3 we repeat measure 1 and the first two beats of measure 2 with a first inversion I add9#11 on Ab, our “tonic” (C, Eb, Ab, Bb, D) followed by the root position Ab6#11 and finally the V maj9.
At this point in measure 4 we have a I add9 in first inversion (C, Ab, Bb, Eb) and a II add9 which would be the actual dominant 7th chord but this example avoids the interval of a tritone found in a chord of that type by simply ascending a whole step up to Bbadd9 in first inversion (D, Bb, C, F).
Our last measure presents a surprise chromatic chord, borrowed from the parallel minor equivalent of the Ab Lydian mode that can be found as the fourth mode of the harmonic minor scale. This mode is commonly known as Lydian b3 b7 or Dorian #4: 1-2-b3-#4-5-6-b7 or (Ab, Bb, Cb, D, Eb, F, Gb,). In a simpler explanation it would be analyzed as bIII maj769 or Bmaj769.
Figure F shows the 12 possible sonorities that can be achieved when using a m7#5 chord with its lowest tone on the 4th string played over the open 5th string as a pedal tone on A. Note names given in the “Chord Spelling” column were chosen to provide a clear idea of what chord tones are found in the “Given Chord” column.
Pedal Tone: A
| Interval From Pedal | Chord Spelling | Given Chord |
| 1 | A-F-G-C | Fadd9 (first inversion) |
| #1/b2 | Bb-F#-Ab-Db | Bbm/maj7#5 (fourth inversion) |
| 2 | B-G-A-D | Bm7#5 (third inversion) |
| b3 | C-G#-Bb-Eb | Am/maj7b9 |
| 3 | C#-A-B-E | Aadd9 |
| 4 | D-A#/Bb-C#-E# | Am11#5b9 |
| #4/b5 | D#-B-C#-F# | A69#11 |
| 5 | E-C-D-G | Am11 |
| #5/b6 | F-C#-D#-G# | Amaj7#5#11 |
| 6 | F#-D-E-A | Dadd9 (second inversion) |
| b7 | G-Eb-F-A# | Am13b5b9 |
| 7 | G#-E-F#-B | Amaj13 |
Figure F: Possible chords by ascending through all intervals from pedal.
To begin the memorization of this concept it is wise to choose some of the more common chord types that you may see in music. These would include m7#5 chords played from the 1, 3, 5, and 7 (coincidentally). Practice these chords using the following procedure:
- Establish a pedal tone; preferably have a friend play a bass note for you while you practice these.
- Play a m7#5 from the root (yields a bVIadd9 in first inversion)
- Play a m7#5 from the 3 (yields a Iadd9, substitute for maj or maj7)
- Play a m7#5 from the 5 (yields a Im11, substitute for m7 or m9)
- Play a m7#5 from the 7 (yields a Imaj13, substitute for maj, maj6, maj7 and maj9)
- Once memorized move to a new root tone a 4th higher than the last.
- Once all keys are played, go back to original starting pedal tone and play chords starting on b2, b3, b5 and b7.
- Repeat using all keys.
- Go back to original starting pedal tone and play chords starting on 2, 4, #5 and 6.
- Repeat using all keys, exercise complete.
The most important part of the above exercise is to hear the sonority produced and know at what distance from the root you can find it. Outside of modal music you will find in practice that chords tend to stay for shorter amounts of time so you may only have the opportunity for one or two substitutions per given chord.
In the final example of Figure 6 we have a different approach to the modal concept where we are superimposing various chords over a static pedal tone of “A”. Numerous sonorities can be created and juxtaposed in a way that would not normally be possible without this pedal tone.
Notice there is primarily one chord shape used in the entire example, the min7#5 with its lowest note on the 4th string, exceptions are found in measures 4 and 8. In the bigger picture it is important to realize how the starting note of these chords will interact with the pedal tone and create new chords of a wide variety.
A logical way to analyze this example is by comparing the lowest chord tone to the pedal tone in terms of intervallic distance. Each measure contains one chord so from the first measure we setup a i m11 (Am11) chord by playing the min7#5 from the 5th above the pedal.
Next we generate a second inversion IV add9 (Dadd9) from a major 6th above the pedal. Measure 3 repeats measure 1 with an Am11, measure 4 yields a bVI maj9 by placing a new chord shape chord a minor 6th above the pedal.
In measure 9 we create a I maj13 chord by playing from the major 7th above the pedal. We then play from an octave above the pedal in measure 14 to get the bVI add9 (Fadd9) in its first inversion. In the 15th measure we play from a 9th above the pedal and generate the I11 (A11) dominant chord and finish in measure 16 with a I add9 (Aadd9) and a 2 harmonics.
There are many possibilities available when using the m7#5 chord including alterations, substitutions and inversions. Overall the sonority of this chord leans toward a modern sound instead of a traditional one.
This is due to the wide interval (#5th) that exists between the 1st and 2nd notes on chords in Figure A and the small interval between notes 2 and 3 (major 2nd). This unique sound of wide interval dissonance combined with small interval dissonance creates a push-pull effect which can yield stunning results.
The chords of Figure B have their own compact sonic character which is created by the use of smaller intervals put in sequential (1-b3-#5-b7) order.
Experiment with these chords and explore the potential that they have to offer. The sooner you can integrate them into your own playing the sooner you can add a new dimension to your sound.
About The Author






The most important thing you missed. How to improvise on this chord. I think you made it unnecessarily complicated
Why make it so complex. Your Minor7#5 sounds like a bVII/3 function-wise. Why not call it this? Most ears will hear it as this? Right?
i lik jazz guitar Your Minor 7#5 sounds likechords,…Thanks,
Hi – another good topic, can you provide pdf’s for these lessons…
Keep ’em coming !
“This is likely due to the fact that it is not a naturally occurring chord in the major scale or any of the principal minor (harmonic, melodic) scales”
isn’t this incorrect?
Fm7#5 can be found in E melodic minor
I have to say. This site is fantastic. It has so much information AND it explains it all in ways that are understandable. Thanks for creating it and sharing it with the rest of us.
No problem – thank you for the comment.